[区域发展] 京津冀经济区内外部经济关联研究——基于地区间投入产出模型的分析(上)
2016年08月17日 来源:国研网 作者:吴三忙 陈炜明 李善同
京津冀经济区包括北京、天津两大直辖市以及河北省,土地面积21.6万平方公里,常住人口约为1.1亿人。尽管京津冀经济区已成长为我国北方经济的重要核心区,与长三角、珠三角并称为我国三大重要增长极。但相较长三角及珠三角,一方面京津冀经济区发展总体较为滞后,2014年京津冀、珠三角、长三角的人均GDP分别为59887元、101408元和80508元,京津冀经济区城镇化率为56.23%,远低于长三角的65%及珠三角的66%,甚至低于东部地区的平均水平59.49%。另一方面,京津冀经济区内部存在较大的发展差距,2014年北京人均GDP达到98966元,天津人均GDP达到105889元,而河北人均GDP仅为39991元。
因此,我国迫切需要加快推进京津冀经济区发展,特别是加快推进京津冀经济区协同发展。事实上,近年来我国已将加快京津冀协同发展上升为国家战略。2015年4月30日,中共中央政治局召开会议,审议并通过了《京津冀协同发展规划纲要》,明确重申推动京津冀协同发展是一个重大国家战略。然而,推进京津冀协同发展面临的一个重要问题是,京津冀经济区内部各地区间经济关联如何?各地区经济如何相互影响?一体化程度是否在深化?京津冀经济区与全国其他地区经济又如何相互影响?对这些问题进行深入研究将为科学制定促进京津冀协同发展的政策奠定基础。
一、文献综述
综合已有文献,对于地区间经济关联及一体化的研究,主要从以下几个方面展开。
第一类:从相关区域内各地区间贸易流量的角度,通过调查地区间贸易流量变化情况来推断地区经济关联及一体化程度,这是使用最早也最常用的方法。1933年,德国著名经济学家盖蒂克和冯·尤恩就在其著作《欧洲生产和经济一体化》中以欧洲各个国家间的贸易流量变化来测算欧洲内部经济关联及经济一体化程度。朱晓军(2008)则使用欧盟商品贸易、服务贸易和外国直接投资密度的变化情况,从不同侧面测算和反映欧盟区域一体化水平的高低。这一方法优点在于其操作简单,且数据获取方便,然而随着地区间一体化程度日益深化,涉及的领域也越来越广泛,如跨地区投资与劳动力转移等,单一地通过贸易流量来量化地区间关联及一体化程度的方法已经不再适用。
第二类:用适当的方法构建合理的经济一体化指标体系,并根据各项指标进行实证分析,综合分析结果以度量经济一体化程度,从一定意义上来说这是对上一种方法的改进和延伸。已有的成果有:娄文龙(2014)采用层次分析法,构建了分四个层次,包含28个指标的经济一体化指标体系,实证分析了京津冀、珠三角、长三角三个经济区域的一体化程度,并将结果进行了对比,发现珠三角经济一体化程度最高。然而由于指标体系建立方式未形成一套统一的标准,受主观影响较大,也未能体现区域内部经济系统复杂运行过程带来的影响,加之数据获取难度较大,从而改进后的方法依然不是一个合适的选择。
第三类:使用不同方法分别研究与地区间经济一体化相关的多个细化层面一体化程度,最后综合各项结果分析地区间经济一体化程度。如刘亚平(2015)从产业一体化、市场一体化、基础设施一体化和公共服务一体化等方面综合评判了江西昌九区域经济一体化发展程度。汪楠(2013)则选取市场一体化、贸易一体化、产业一体化以及城乡一体化这四个指标对北部湾经济区四市(南宁、北海、钦州、防城港)之间经济一体化程度进行了评估。
第四类:利用投入产出表来测算地区间经济关联情况,并分析地区间经济一体化程度。如张艳(2012)基于投入产出表对中国参与东亚经济的一体化程度进行了实证研究。而李秀敏,赵晓旭(2008)利用边界效应模型和中国地区间投入产出表的数据对中国市场一体化的程度进行了分析。投入产出表可以全面系统地反映国民经济各部门之间的投入产出关系,揭示生产过程中各部门之间相互依存和相互制约的经济技术联系,因此在研究地区间经济一体化方面有其独特的优势。另外,该方法不仅能详细地展现地区间复杂的经济联系,还能测算出该区域与区外的经济联系。
除上述方法外,还有学者运用了其他一些方法对地区间经济一体化程度进行了研究,如刘云中,刘泽云(2011)通过观察各个地区间经济波动一致性程度的变化来度量地区间经济的一体化,构建了地区间经济一体化指数,并由此刻画了我国经济一体化程度的变化轨迹。唐文琳,李雄师(2014)基于时序主成分分析框架,构建起区域经济一体化程度测量模型,对中国—东盟区域经济一体化程度在2002—2012年的变化情况进行了测量,结果表明:总体上看,中国—东盟区域经济一体化程度有了明显的提升。
考虑到地区(省、区、市)之间主要联系是地区间贸易,地区间贸易量越大,表明地区间经济联系越紧密,一体化程度越高。因此分析地区间经济联系,地区间贸易量是重要分析变量。然而,从地区最终需求角度来考虑,地区间贸易并不是最终需求,某一地区向国内其他地区调出商品,是由其他地区消费、投资和出口衍生出对于该地区的中间需求。因此,地区间贸易可以进一步分解为调出地区(或者第三方省份)的最终消费、投资和出口需求。从这个角度而言,调出地区的最终需求事实上包括两部分:一部分是本地区的三大最终需求驱动的;另一部分是由于地区间贸易的存在,由其他地区的三大最终需求驱动的。因此,分析两个地区间经济联系或一体化程度,事实上仅需要分析两个地区之间最终需求的相互影响程度。以A和B两个地区为例,如果A地区从B地区调入大量商品,本质上是A地区消费、投资和出口需求对B地区的衍生需求拉动。A地区消费、投资和出口需求对B地区的衍生需求拉动越强,表明A地区对B地区经济发展影响越大。综合以上分析,分析地区间经济联系,可以分析地区间消费、投资和出口需求三大最终需求的相互影响,而对地区间最终需求相互影响进行分析,尤其是地区经济发展对其他地区经济的带动作用和溢出、反馈效应是地区间投入产出模型的优势(陈锡康,杨翠红,2011)。
基于前述分析,本文基于地区间投入产出模型,构建测算某地区消费、投资及出口三大最终需求对其地区经济拉动作用的方法,利用1997年、2002年、2007年三个年份的我国地区间投入产出表,测度北京、天津、河北三地区各自的消费、出口、投资对其他两个地区的拉动作用,并分析京津冀与全国其他地区的相互拉动作用,由此分析京津冀内部经济关联状况及京津冀与全国其他地区经济关联状况。
二、研究方法和数据来源
(一)地区间投入产出模型
从20世纪后半叶以来,投入产出模型已经被应用于一个国家内部不同地区的研究。Miller and Blair(1985)认为以一国内部地区层面存在两个典型的特征使得利用地区间投入产出模型进行分析成为必要:其一,就是一国各地区具有不同的生产技术特征,地区之间可能接近,抑或相距甚远,但是不会完全相同,这在投入产出表中就表现为不同中间投入结构;其二,就是一国内部地区对外部经济的依赖,这不仅表现为国际贸易,也表现为国内贸易。正是因为如此,地区间投入产出模型成为研究区域问题非常重要的工具。
从投入产出模型的理论来看,Isard提出的地区间投入产出模型(Inter regional Input-Output tables/models)是最为理想的地区间经济联系分析工具,该投入产出表不仅包含地区内部的经济联系,而且拥有十分详细的地区经济联系,能够明确各地区每一种用途的商品来源。但是在现实中,由于很难收集这种非常翔实的贸易数据,因此,很少有研究采用Isard提出的地区间投入产出模型。为了克服这一数据收集的难点,Chenery(1953)和Moses(1955)分别提出了Multi-regional input-output model(MRIO模型),也称为Chenery-Moses模型或列系数模型。该模型假设各地区不同用途(不同部门的中间投入、最终消费和投资)的商品其来源构成是一样的①。因此,对地区间的贸易数据只需要了解生产地和使用地,而无须了解该贸易品是被用于哪个部门,还是被用于最终消费或投资,这大大地减少了数据的需求量。因此,本文将采用Chenery和Moses提出的MRIO模型②。
假定一国内部有n个地区,m个生产部门,进一步假设每个产业只生产一种产品(反之亦然)。因此,从需求角度而言,区域r部门i产品的总需求可以用以下方程表示:

其中,i、j表示生产部门(i,j=1,…,m),r、s表示地区(r,s=1,…,n)。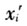 表示地区r部门i产品的总需求/产出③;
表示地区r部门i产品的总需求/产出③;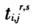 表示地区s部门j对区域r部门i产品的中间投入需求;
表示地区s部门j对区域r部门i产品的中间投入需求;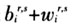 表示地区s对地区r部门i产品的国内最终需求(最终消费加投资);
表示地区s对地区r部门i产品的国内最终需求(最终消费加投资);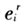 地区r部门i产品的出口需求。
地区r部门i产品的出口需求。
从公式(1)可以看出,一个地区产品需求不仅包含地区内部中间投入需求和最终需求,还包含国内其他地区对该地区产品的中间投入需求和最终需求,另外还包含该地区的出口需求。
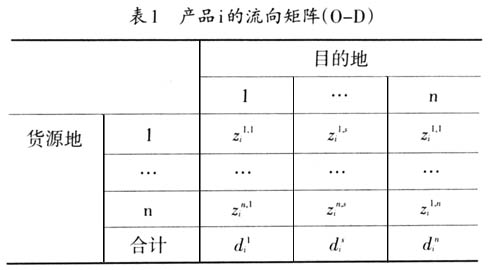
地区间投入产出模型中最为关键的就是产品流向O-D矩阵。基于O-D矩阵,可以得到贸易系数,即每一地区每种用途产品来源的地区构成或每一地区每种产品去向的地区构成。因此,本文采用MRIO模型,其假设目的地区各种用途的产品来源构成是相同的。将O-D矩阵各元素除以其列之和,就可以可得到相应的贸易系数,即可以测算地区r对产品i的总需求由本地区提供的比例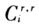 和由其他地区供给的比例
和由其他地区供给的比例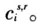
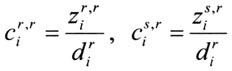
利用各地区的投入产出表,还可以得到各地区对国内产品的中间投入技术系数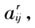 该系数反映地区r生产单位产品j对各地区国内i产品的投入需求,即包括来自本地区的产品,也包括来自国内其他地区的产品(Moses,1955)。具体用公式表示:
该系数反映地区r生产单位产品j对各地区国内i产品的投入需求,即包括来自本地区的产品,也包括来自国内其他地区的产品(Moses,1955)。具体用公式表示:
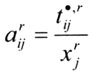
其中,符号·表示对所有来源地区的汇总。将贸易系数和中间投入系数代入公式(1),可以得到如下公式:
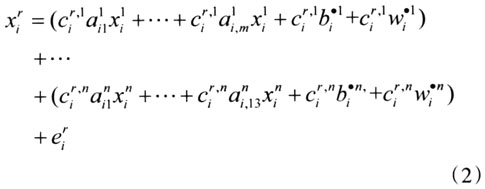
其中,i=1,…,13。公式(2)可以改写出矩阵形式,即:
X=CAX+C(B+W)+E (3)
其中X表示产出矩阵,C为贸易系数矩阵,A为国内的中间投入系数矩阵,B为最终消费矩阵,W为投资矩阵,E为出口矩阵。
进一步改写公式(3)可以得到公式(4),
X=CAX+C(B+W)+E⇒(I-CA)X=C(B+W)+E⇒X=(I-CA)-1(CB+CW+E) (4)
公式(4)就可以用来做模拟分析,即可以测算各种最终需求(包括消费、投资和出口)对总产出的拉动作用。
引入各部门的增加值率,可以进一步分解得到地区r最终需求对对地区s的增加值拉动,以地区r出口需求对地区s的增加值拉动为例,其中
VAEs,r=V(I-CA)-1Er…… (5)
E为地区r出口矩阵,V为地区s各部门增加值率矩阵,为地区r出口拉动地区s的增加值,矩阵元素形式如下:

vae为地区r出口拉动地区s部门i的增加值。因此,地区r出口拉动地区s的增加值总和为:
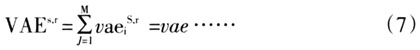
使用上述方法可以测算出一个地区消费、投资、出口三个最终需求对另一个地区增加值的拉动作用。